Understanding Eyeglass Prescriptions
Eyeglass prescriptions consist of several key values that correct different vision problems. This guide breaks them down to help you understand each part and what it means for your vision.
Prescription Components Explained
| Component | Definition | Purpose |
|---|---|---|
| Sphere (SPH) | Indicates the degree of nearsightedness (−) or farsightedness (+). | Helps focus light directly on the retina. |
| Cylinder (CYL) | Corrects astigmatism, caused by an irregularly shaped cornea. | Refines how light enters the eye in specific meridians. |
| Axis | Direction (0°–180°) of astigmatism correction. | Aligns the cylindrical correction properly. |
| ADD | Extra magnifying power for reading or close work. | Used in bifocals, progressives, or reading glasses. |
| Prism | Shifts image position to aid eye alignment. | Helps correct double vision or eye muscle imbalance. |
| Base Direction | Direction of prism (e.g., base in, base up). | Determines the image shift direction. |
How Plus and Minus Lenses Work
| Lens Type | Function | Light Behavior |
|---|---|---|
| Plus Lenses | Used for hyperopia (farsightedness) | Converge light; thicker center, thinner edges |
| Minus Lenses | Used for myopia (nearsightedness) | Diverge light; thinner center, thicker edges |
Think of plus lenses as two prisms joined at the base and minus lenses as two prisms joined at the apex.
Transposing a Prescription
Sometimes, a prescription may be written in plus cylinder form (used by ophthalmologists) or minus cylinder form (used by optometrists). You can convert between them using the following steps:
- Add the sphere and cylinder to get the new sphere.
- Change the sign of the cylinder.
- Adjust the axis by 90°, staying within 0°–180°.
Example: Transpose −1.00 −1.00 ×090 → −2.00 +1.00 ×180
The Optical Cross
Same power (steepness/thickness) all the way around
The optical cross shows the power of a lens in different meridians, mainly 090 degrees apart from each other. This is power, not necessarily prescription. You can put a prescription into an optical cross or you can understand the prescription of a lens from an optical cross. For example a spherical lens with a power of -5.00 will have the same power in all meridians and will look like this on an optical cross. Because there is no change in power at any point in this lens it is safe to say that there is no CYL power on this lens.
Different powers (thickness/steepness) in different meridians
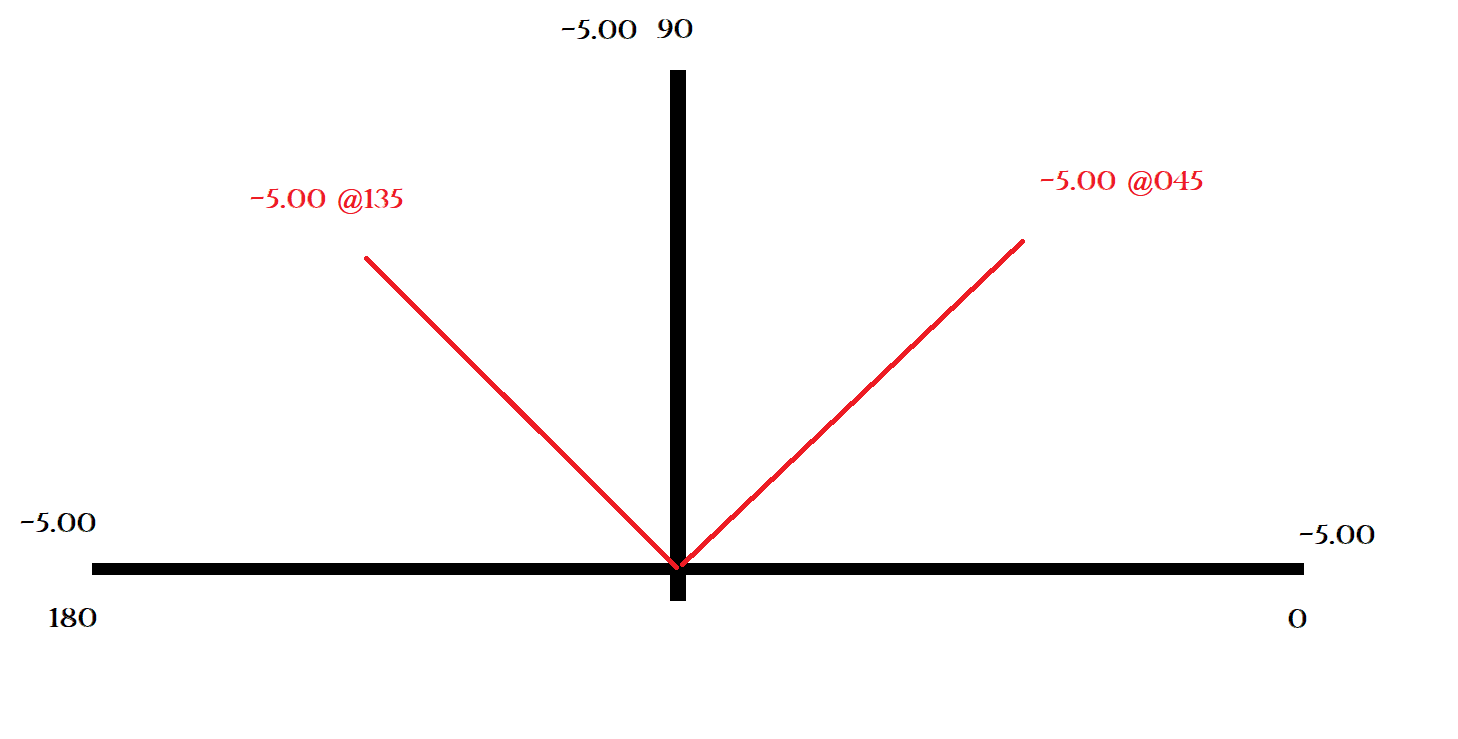
When you compare a spherical lens to a lens that has Cylinder power (to correct for astigmatism) you will see that a cylinder lens will have two different powers and thicknesses 090 degrees apart from each other. The lenses thinnest point will be 090 degrees away from it’s thickest point and will look like this on an optical cross. Let’s use this power, -4.00 -1.00 045 as an example. The difference in power 090 away from each other gives the CYL power of the lens. In the example here you see a difference of -1.00 when you go from -4.00@045 to -5.00 @135 and you see a +1.00 CYL power when you go from -5.00 @135 to -4.00 @045.
A Quote from John Seegers that may help you understand the optical cross and something great to memorize.
“The Shorter the Radius the Steeper the Curve, The Steeper the curve the higher the power, The Higher the power the thicker the lens.”
Example 1
A lens with a power of -2.50 @ 060 and a power of -1.50 090 degrees away (150) can be written onto an optical cross like this.
The power of the lens has a difference of +1.00 090 away when moving from -2.50 @060 to -1.50 @150
-2.50 to -1.50 is +1.00 (this difference is the CYL power) and can be written out as;
-2.50 +1.00 060
The power of lens has a difference of -1.00 090 away when moving from -1.50 @150 to -2.50 @060
-1.50 to -2.50 is -1.00 (this difference is the CYL power) and can be written out as;
-1.50 -1.00 150
Example 2
Let’s say you have these two powers -12.00 @045 and -6.00 @135. How would you put this into an optical cross and how would you write this out in RX form? The difference in power in either direction 6.00 diopters. It is plus 6.00 diopters when moving from -12.00 to a -6.00 and minus power when moving from -6.00 to -12.00. It can be written as
6.00 diopters difference @090 away
-6.00 -6.00 045 or -12.00 +6.00 135 and on an optical cross it would look like this.
Example 3
Now let’s work backwards from an optical cross into written form. Let’s say you have the following optical cross and you want to know how to write out the power.
Start with either meridian and write the power in that meridian as the sphere power and your axis at that point. For this example you see that there is -3.75 @045 so we now have two parts, the sphere power and the axis. We just need the CYL power and we are done! So far we have -3.75 _______ 045.
Next, calculate the power difference moving 090 degrees away and write that out as your CYL power. At 090 away the power is -4.25, because this power is MORE minus the CYL power is minus. There is an additional -0.50 power going from -3.75 to -4.25. You can write the -0.50 into your power so you now have -3.75 -0.50 045.
Let’s also try starting from the power at 135 degrees. We have -4.25 @135 and this can be written out as -4.25 ________ 135. When moving from -4.25 to -3.75 you are becoming LESS minus (or adding plus power) so your CYL is now in PLUS form. The power can be written out as -4.25 +0.50 135
Checking your work!
Transpose your written power to see if it matches up to the optical cross. This is a great way to double check your work. Another tip is to make sure you work from both meridians just to double check your math and power signs.
Concept of Axis from Laramy-K